线性回归基础概念
机器学习中的两个常见的问题:回归任务和分类任务。在监督学习中(也就是有标签的数据中),标签值为连续值时是回归任务,标志值是离散值时是分类任务。而线性回归模型就是处理回归任务的最基础的模型。
- 线性关系:两个变量之间的关系是一次函数关系的——图象是直线,叫做线性;
- 非线性关系:两个变量之间的关系不是一次函数关系的——图象不是直线,叫做非线性。
- 回归分析:人们在测量事物的时候因为客观条件所限,求得的都是测量值,而不是事物真实的值,为了能够得到真实值,无限次的进行测量,最后通过这些测量数据计算回归到真实值,这就是回归的由来。
线性回归的数学表示与原理
直接讨论多变量情形。设 y 是关于 x 的 n 维线性变量,有 m 个样本。那么我们要求的回归函数为:\(h_\theta (x) = \theta _0 + \theta _1 x_1 + \theta _2 x_2 + \cdots + \theta _n x_n = \sum\limits_{i = 0}^n \theta _i x_i = \underline \theta ^T \underline x \),其中\(\underline \theta ^T = \left[ \theta _0, \theta _1, \theta _2, \cdots , \theta _n \right]\), \(\underline x = \left[ 1, x_1, x_2, \cdots x_n \right]^T\)。
定义损失函数\(J\left( \theta _1, \theta _2, \cdots , \theta _n \right) = \frac{1}{2m}\sum\limits_{i = 1}^m \left[ \left( h_\theta \left( x^{(i)} \right) – y^{(i)} \right)^2 \right]\)
梯度下降法求解线性回归
在一元函数中叫做求导,在多元函数中就叫做求梯度。梯度下降是一个最优化算法,通俗的来讲也就是沿着梯度下降的方向来求出一个函数的极小值。比如一元函数中,加速度减少的方向,总会找到一个点使速度达到最小。通常情况下,数据不可能完全符合我们的要求,所以很难用矩阵去求解,所以机器学习就应该用学习的方法,因此我们采用梯度下降,不断迭代,沿着梯度下降的方向来移动,求出极小值。梯度下降法包括批量梯度下降法和随机梯度下降法(SGD)以及二者的结合 mini 批量下降法(通常与 SGD 认为是同一种,常用于深度学习中)。
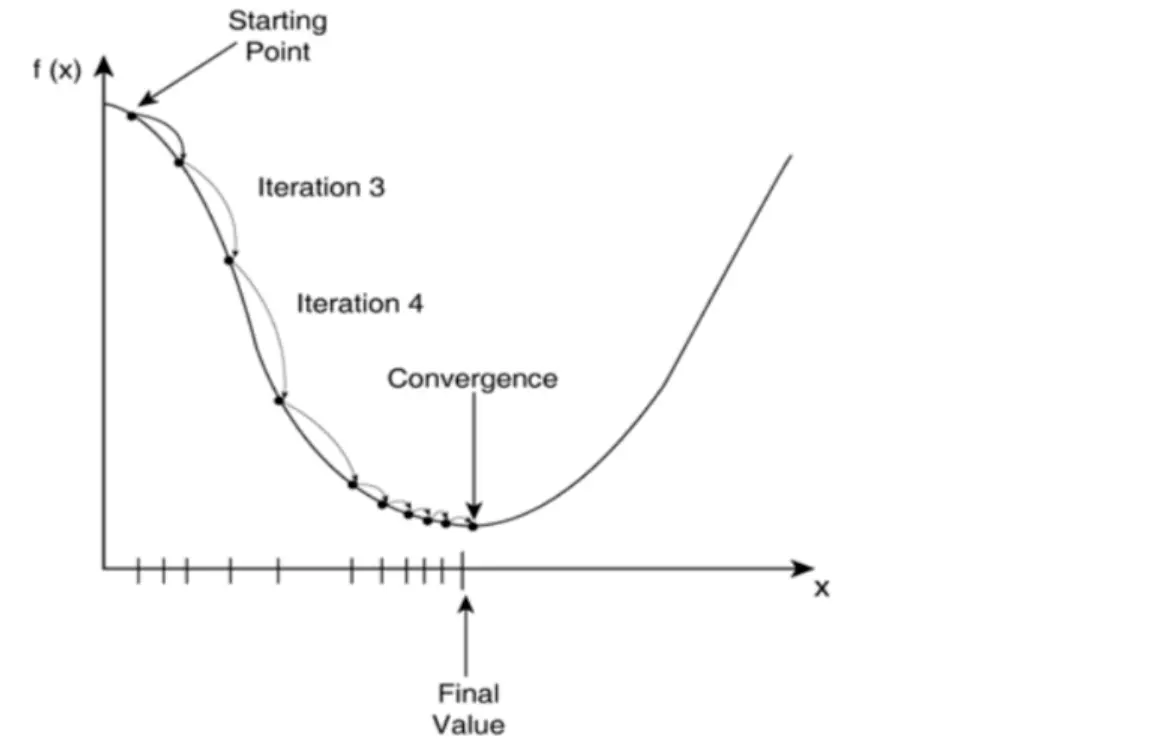
求解过程如下:
- 初始化\(\theta\)
- 求\(\frac{\partial J(\theta )}{\partial \theta }\):\(\frac{\partial J(\theta )}{\partial \theta _j} = \left( h_\theta (x) – y \right) x_j\)
- 更新\(\theta\):\(\theta _j = \theta _j – \alpha \frac{\partial J(\theta )}{\partial \theta _j}\),其中\(\alpha \)称为学习率,是一个参数
线性回归拟合问题与解决方案
欠拟合和过拟合问题
\(\alpha \)过小可能导致欠拟合,\(\alpha \)过大可能导致过拟合:
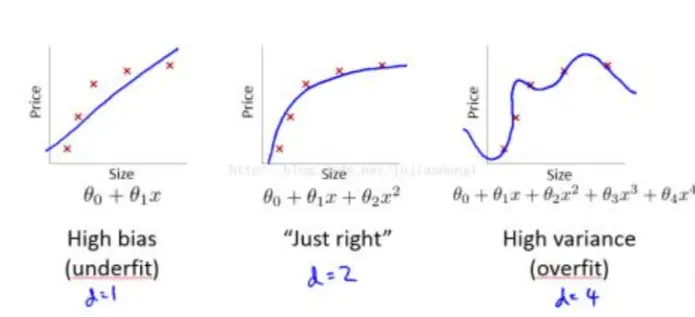
正则化解决方法
添加一个正则化项,即梯度下降公式添加一个参数造成扰动:
\(J\left( \theta _1, \theta _2, \cdots , \theta _n \right) = \frac{1}{2m}\sum\limits_{i = 1}^m \left[ \left( h_\theta \left( x^{(i)} \right) – y^{(i)} \right)^2 + \lambda \sum\limits_{j = 1}^n \theta _j^2 \right]\)
Python 实现线性回归模型
使用 NumPy 向量化计算
一元线性回归实现
import numpy as np
# 生成示例数据
x = np.array([1, 2, 3, 4, 5], dtype=np.float64)
y = np.array([2, 3, 4, 5, 6], dtype=np.float64)
# 添加偏置项(将 x 转换为 [x, 1] 形式,方便矩阵运算)
X = np.vstack([x, np.ones(len(x))]).T # 形状:(n_samples, 2)
# 最小二乘法求解:w = (X^T X)^(-1) X^T y
w, b = np.linalg.inv(X.T @ X) @ X.T @ y
print(f"NumPy 计算:w = {w:.2f}, b = {b:.2f}")多元线性回归实现
import numpy as np
# 1. 生成示例数据(多元特征)
np.random.seed(42) # 固定随机种子,确保结果可复现
n_samples = 100 # 样本量
n_features = 3 # 特征数(自变量数量)
# 特征矩阵 X:形状 (n_samples, n_features)
X = np.random.randn(n_samples, n_features) # 随机生成符合正态分布的特征
# 真实参数(用于构造标签 y)
true_weights = np.array([2.3, -1.5, 0.8]) # 3 个特征的权重
true_bias = 1.2 # 偏置项
# 生成标签 y = X·weights + bias + 噪声(模拟真实数据)
y = X @ true_weights + true_bias + np.random.randn(n_samples) * 0.5 # 噪声标准差 0.5
# 2. 构造包含偏置项的特征矩阵 X_b(在 X 后加一列全为 1 的向量)
# 形状变为 (n_samples, n_features + 1),最后一列对应偏置项的系数
X_b = np.hstack([X, np.ones((n_samples, 1))])
# 3. 用最小二乘法求解参数(包含权重和偏置)
# 公式:w = (X_b^T · X_b)^(-1) · X_b^T · y
XT_X = X_b.T @ X_b # X_b 的转置与 X_b 的乘积
XT_y = X_b.T @ y # X_b 的转置与 y 的乘积
w = np.linalg.inv(XT_X) @ XT_y # 求解参数向量(包含权重和偏置)
# 4. 提取结果
estimated_weights = w[:-1] # 前 n_features 个是特征权重
estimated_bias = w[-1] # 最后一个是偏置项
# 5. 输出对比
print("真实参数:")
print(f"权重:{true_weights}")
print(f"偏置:{true_bias}\n")
print("拟合参数:")
print(f"权重:{estimated_weights.round(4)}")
print(f"偏置:{estimated_bias.round(4)}\n")
# 6. 预测与误差评估
y_pred = X_b @ w # 矩阵乘法计算预测值
mse = np.mean((y - y_pred) **2) # 均方误差(越小越好)
print(f"均方误差(MSE):{mse:.4f}")使用 Scikit-learn 库实现
一元线性回归实现
from sklearn.linear_model import LinearRegression
import numpy as np
# 示例数据(注意:sklearn 要求 x 为二维数组)
x = np.array([1, 2, 3, 4, 5]).reshape(-1, 1) # 形状:(n_samples, 1)
y = np.array([2, 3, 4, 5, 6])
# 创建并训练模型
model = LinearRegression()
model.fit(x, y)
# 提取参数
w = model.coef_[0] # 斜率
b = model.intercept_ # 截距
print(f"Scikit-learn 计算:w = {w:.2f}, b = {b:.2f}")
# 预测
y_pred = model.predict(x)
print("预测结果:", y_pred)多元线性回归实现
from sklearn.linear_model import LinearRegression
import numpy as np
# 同上的示例数据
np.random.seed(42)
X = np.random.rand(10, 3) # 3 个特征
true_w = np.array([2.5, -1.8, 3.2])
true_b = 4.0
y = X @ true_w + true_b + np.random.normal(0, 0.1, 10)
# 创建并训练模型
model = LinearRegression()
model.fit(X, y) # X 无需手动加偏置项,模型会自动处理
# 提取参数
w = model.coef_ # 权重:[w1, w2, w3]
b = model.intercept_ # 偏置项
print("真实参数:w1=2.5, w2=-1.8, w3=3.2, b=4.0")
print(f"拟合参数:w1={w[0]:.2f}, w2={w[1]:.2f}, w3={w[2]:.2f}, b={b:.2f}")
# 预测
y_pred = model.predict(X)
print("\n 预测值:", y_pred.round(2))
print("真实值:", y.round(2))线性回归模型效果评估指标
均方误差(Mean Squared Error, MSE)
定义:预测值与真实值差值的平方的平均值。
公式:$$ \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i – \hat{y}_i)^2 $$
其中 \( y_i \) 是真实值,\( \hat{y}_i \) 是预测值,\( n \) 是样本量。
原理:通过平方放大误差的影响(尤其对 outliers 更敏感),使模型更关注大误差的修正,值越小说明拟合效果越好。
特点:单位是因变量单位的平方,不直观,但数学性质稳定,是回归模型最基础的损失函数。
均方根误差(Root Mean Squared Error, RMSE)
定义:MSE 的平方根。
公式:$$ \text{RMSE} = \sqrt{\text{MSE}} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i – \hat{y}_i)^2} $$
原理:将 MSE 的单位还原为与因变量一致(如因变量单位是”元”,RMSE 单位也是”元”),更直观地反映平均误差大小,值越小越好。
特点:继承了 MSE 对大误差的敏感性,同时具备可解释性。
平均绝对误差(Mean Absolute Error, MAE)
定义:预测值与真实值差值的绝对值的平均值。
公式:$$ \text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |y_i – \hat{y}_i| $$
原理:直接衡量误差的平均大小,对异常值的敏感度低于 MSE/RMSE(因未平方),值越小越好。
特点:单位与因变量一致,但数学性质不如 MSE(如绝对值函数在 0 点不可导,不利于优化)。
决定系数(Coefficient of Determination, \( R^2 \))
定义:模型可解释的因变量变异占总变异的比例。
公式:$$ R^2 = 1 – \frac{\sum_{i=1}^{n} (y_i – \hat{y}_i)^2}{\sum_{i=1}^{n} (y_i – \bar{y})^2} $$
其中 \( \bar{y} \) 是因变量的平均值。
原理:
- 分母是”总平方和(TSS)”,代表因变量本身的总变异(不考虑模型时的误差);
- 分子是”残差平方和(RSS)”,代表模型未解释的变异(预测误差);
- \( R^2 \) 越接近 1,说明模型解释的变异越多,拟合效果越好。
特点:
- 取值范围通常在 [0, 1](极端情况可能为负,此时模型效果差于直接预测均值);
- 不受因变量单位影响,可跨不同问题对比,但对特征数量敏感(增加无关特征可能虚高 \( R^2 \))。
调整后的 \( R^2 \)(Adjusted \( R^2 \))
定义:对 \( R^2 \) 的修正,消除特征数量对结果的干扰。
公式:$$ R^2_{\text{adj}} = 1 – \frac{(1 – R^2)(n – 1)}{n – k – 1} $$
其中 \( k \) 是特征数量,\( n \) 是样本量。
原理:当增加无关特征时,\( R^2 \) 可能不变或略增,而调整后 \( R^2 \) 会惩罚过多的特征(分母随 \( k \) 增大而减小,导致整体值下降),更客观反映模型对未知数据的拟合能力。
特点:比 \( R^2 \) 更适合多元回归,尤其当特征数量较多时。